Quantum Computing Innovation for Off-Road Mobility

Project begins Sep. 2020.

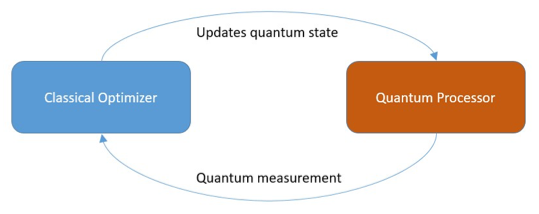
Recent impressive progress in quantum technology, particularly in programmable quantum computers, has invigorated a renewed interest in quantum algorithm research. This excitement is largely fueled by the existence of quantum algorithms exhibiting exponential speedups compared to the best-known classical algorithms (such as Shor factoring). Furthermore, plausible complexity-theoretic assumptions strongly suggest that quantum computers are capable of preparing quantum states which are hard to sample classically.

An important consideration in quantum algorithm design is the ability to perform fault-tolerant quantum computation, which necessarily incurs an overhead in the requisite number of physical qubits. Although, these overheads are expected to be polylogarithmic in the asymptotic limit of problem size, they are well beyond the near-term capabilities for problem sizes of technological importance. Interest has thus shifted to hybrid quantum-classical algorithms which involve the optimization of parameters of a variational quantum circuit to prepare a desired target quantum state (see figure). These variational algorithms exploit the advantages of a Quantum Processing Unit (QPU) for state preparation as well as a Classical Processing Unit (CPU) for optimization purposes. The interaction of a QPU and CPU in this way can plausibly deliver a quantum advantage and variational algorithms have been designed for solving hard combinatorial optimization as well as quantum chemistry problems.

A theoretical obstacle facing variational quantum algorithms is that they involve the introduction of a stochastic optimization problem as part of the classical outer loop. This optimization problem is generically non-convex, which greatly complicates the asymptotic complexity analysis. Although asymptotic speedups appear out of reach, it is nevertheless plausible that hybrid quantum-classical algorithms could provide valuable heuristics for solving problems of practical interest. Moreover since they involve stochastic optimization, they exhibit noise robustness and can be implemented on noisy intermediate-scale quantum computers with limited number of qubits.

The primary objective is to develop Quantum algorithms for tackling hard computational problems arising in the field of autonomous ground vehicle systems research. In particular, we will explore the quantum approximate optimization landscape through the lens of information geometry, exploiting the strong analogy between quantum circuit architectures and deep neural networks. Specifically, we will draw on a toolbox of recently developed quantum-information-geometric optimization tools which have proven successful in Machine Learning and digital quantum computation.

In parallel to this research, we will pursue classical algorithms for enabling the simulation of our quantum algorithms on foreseeable quantum hardware. The main tool we will utilize for this purpose is the Variational Monte Carlo (VMC), which simulates variational quantum states using neural networks. The use of VMC as a stepping stone will yield valuable lessons about the optimization dynamics, which can be imported to the quantum computing literature upon the availability of quantum hardware.

Publications:

• Yabin Zhang, David Gorsich, Paramsothy Jayakumar and Shravan Veerapaneni. Continuous-variable Optimization with Neural Network Quantum States. Quantum Machine Intelligence 4, 9, 2022. https://doi.org/10.1007/s42484-022-00067-z

References:

• Dan Shepherd and Michael J Bremner. Temporally unstructured quantum computation. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 465(2105):1413–1439, 2009.
• Robert Raussendorf and Jim Harrington. Fault-tolerant quantum computation with high threshold in two dimensions. Physical review letters, 98(19):190504, 2007.
• Edward Farhi, Jeffrey Goldstone, and Sam Gutmann. A quantum approximate optimization algorithm. arXiv preprint arXiv:1411.4028, 2014.
• Alberto Peruzzo, Jarrod McClean, Peter Shadbolt, Man-Hong Yung, Xiao-Qi Zhou, Peter J Love, Al´an Aspuru-Guzik, and Jeremy L O’brien. A variational eigenvalue solver on a photonic quantum processor. Nature communications, 5:4213, 2014.
• Bobak Toussi Kiani, Seth Lloyd, and Reevu Maity. Learning unitaries by gradient descent. arXiv preprint arXiv:2001.11897, 2020.
• John Preskill. Quantum computing in the nisq era and beyond. Quantum, 2:79, 2018.
• James Stokes, Josh Izaac, Nathan Killoran, and Giuseppe Carleo. Quantum natural gradient. arXiv preprint arXiv:1909.02108, 2019.
• Shun-Ichi Amari. Natural gradient works efficiently in learning. Neural computation, 10(2):251–276, 1998.

# 1.A73